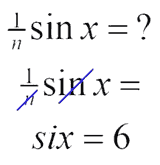Growing Outta Control

e might seem like an odd number at first, but it has a lot of special properties that makes it worth knowing about. It can be used to construct perfect arches, calculate continuous interest, and plot a trip where the distance you have traveled is always the same as your speed, which is always the same as your acceleration. It creates the ultimate exponential, growing without bound.

e's Spiffy Properties

• the first mention of e occurs in 1618
• e is used to find interest that is accumulated continuously, the method commonly used by banks
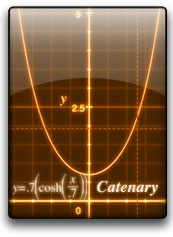
• an equation involving e describes a catenary, the shape of hanging cords that are flexible but not stretchy
• the Gateway Arch in St Louis, Missouri has the shape of an upside down catenary
• e is involved in the equation for the statistical bell curve
• The sum
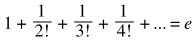
• The area underneath 1/x from 1 to e is 1
• e is irrational, because it cannot be expressed as a fraction of whole numbers
• e is transcendental, because there is no polynomial with rational coefficients of which e is a root
• the value of e^x at any point is the same as its slope at that point
• the infinite digits of e have no pattern