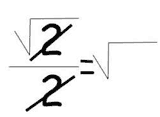Benford's Law

The Man Behind Discovery

Simon Newcomb is a mathematician and accomplished astronomer born in Wallace, Nova Scotia. Although he had no formal education aside from his father and a brief apprenticeship with an herbalist, he went on to be a well respected professor of mathematical astronomy, writing several textbooks, becoming a founding member and the first president of the American Astronomical Society, and serving as president of the American Mathematical society.

An Eye Catching Oddity

In 1881, Newcomb was looking at a book of log tables, and he noticed that certain pages were more worn than others. The pages with numbers of leading digit 1 seemed to be dirtier and more worn the the subsequent pages.

The Theory!

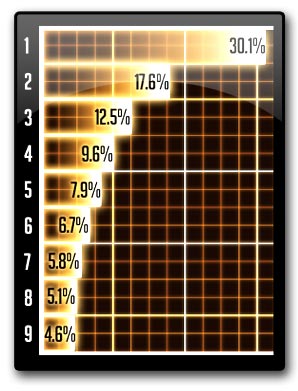
Newcomb theorized that given a set of measurements, numbers with 1 as a leading digit occur more often than numbers of any other leading digit. In fact, he determined that the probability of having a leading digit n is log(n+1/n).

So the larger the leading digit, the less likely it was to occur. This discovery was met with a lack of interest and was largely overlooked.

The Benford Revival

This first digit law was later revived in 1938 by a physicist named Frank Benford. He verified the phenomenon on varied and numerous sets of data. His investigation of this first digit property was so thorough, that it is now known as "Benford’s law".

Collecting Data

So if you collect all the measurements you can find on river lengths, river areas, baseball batting averages, country areas, the figures in Bill Clinton’s tax returns, properties of chemicals, or even the house numbers of everyone named john, numbers starting with 1 will occur about 30% of the time.

So, everyday sources of naturally generated numbers follow the pattern outlined by Benford’s law. In fact, it is scale invariant; it doesn’t matter if you measure something in meters or feet or inches or furlongs, the law continues to hold. This is good, because we would expect a law like this to be independent of scaling.

Disbelief

But this is mind boggling! Why should this work? I would have expected that the numbers starting with one should occur as often as any other number, with a probability of 1/9.

Think of it this way. If you have a measurement of 1000, you would need a 100% increase to take that measurement from 1000 to 2000. But, to make it from 2000 to 3000, you would only need a 50% increase, and from 3000 to 4000 only about 33%. This amount of increase from one leading digit to the next gradually decreases, with finally 9000 needing only 11% to get back to 10000. And again, you would need to increase 10,000 by 100% to get to the next leading digit. So this is why leading digits are distributed in this way. The larger the leading digit, the closer it is to its neighbor, probabilistically.

A New Way to Pick Lottery Numbers?

Now, I can see what you are thinking, maybe this is the key to getting rich: only choose lottery numbers that start with 1. Well, not exactly.

Lottery numbers are truly random, with each digit having equal probability of getting chosen. These numbers are not naturally occurring data, their properties are controlled.

Average Canadian Male Height

Ok, so where else does Benford’s law not apply? Look at the heights of all the males in Canada: it averages about 70 inches (5’10’’). I can comfortably say with few exceptions that most males are between 60 inches and 80 inches. So probably 99% of these heights have a leading digit of 6 or 7, and you would be extremely hard pressed to find someone who is 10 inches or 100 inches tall. This is because male heights are normally distributed about a mean (average value), and the heights do not span much more than 2 leading digits with any frequency.

Where Not to Use Benford's Law

So, Benford’s law doesn’t apply to purely random numbers like lottery numbers, or random numbers that are normally distributed about a mean. You can only look at naturally occurring measurements.

Practical Use?

Benford’s law is used by forensic accountants as a method to spot fraud. If we look at a company’s account information, all the figures should follow the leading digit distribution outlined by this law. A deviation from this distribution could be evidence that a company is cooking its books, and that further investigation is warranted.