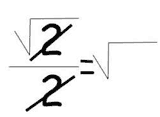The History of π
π comes on the scene
π is the ratio of the circumference of a circle to its diameter. This makes π a very useful number for constructing and measuring circular structures, so we have thought about π for a very long time.
Ancient approximations
Early references to π in India are found in texts describing how to build alters. We know what value the ancient Egyptians used for π because of a solution to squaring the circle found in the Rhind Papyrus.
A problem of the ancient times, squaring the circle asked if you could create a circle with the same area as a square using only an unmarked straight edge and a compass. This was proved to be impossible, but only much later. The solution for this unsolvable problem gives a value of π that isn’t correct, but it’s quite close
At about the same time the Babylonians were using 3 1/8 as an approximation, which is a little bit closer. A passage of the Bible written in 550 BCE describes a circular fountain with dimensions that indicates pi as 3.
Archimedes’ method
Archimedes (287-212 BC) managed to get a pretty good idea of π’s value, and wisely didn’t claim to know it exactly. His method (described in Finding the Digits) of using regular polygons to approximate a circle was used for at another 1800 years, even after other methods were developed. The accuracy got better and better as better algorithms were developed for the calculations, which allowed calculations with polygons with more and more sides.
In 1610 Ludolph van Ceulen managed to calculate π to 35 decimal places. He used the method of Archimedes, but managed a much greater degree of accuracy by using a polygon with 262 sides. His dedicated work bordering on obsession gave π the name Ludolph’s number, which is still occasionally used.
Infinite Series
In 1579 Viéte created the first infinite series as a way to calculate π. This was the first infinite product, a series that got closer and closer to π the more terms of the series you calculated. The idea of infinite series and limits is connected with the development of calculus, a major change in mathematics. This opened new doors for faster ways to calculate π.
Proving the Properties of π
Important advances in our understanding of π came when Johann Lambert proved, in the late 18th century, that π is irrational and that it cannot be a repeating pattern of digits. Ferdinand von Lindemann proved in 1882 that π is transcendental (is not a root of any polynomial with rational coefficients), and used this result to prove once and for all that the ancient problem of squaring the circle is impossible.
Finally some calculating help
In the late 1940s calculators greatly sped up the calculation of π, and then the invention of electronic computers changed everything, eliminating the human limitations involved with the massive amount of calculations of π. The focus was now on developing elegant formulas and the algorithms computers use to calculate them. By 1973 a million digit approximation had been calculated, and in 1989 a billion digits was reached. The current record is a bit more than 1.2 trillion digits, calculated in 2002 using a supercomputer calculating for about 600 hours.
Do We Really Need That Many Digits?
Knowing that many digits of π isn’t useful in any of the calculations that we will ever do. As the mathematician Simon Newcomb (1835 - 1909) said: “Ten decimal places of pi are sufficient to give the circumference of the earth to a fraction of an inch, and thirty decimal places would give the circumference of the visible universe to a quantity imperceptible to the most powerful microscope.” Calculating the digits of π has instead become a way to test the speed and efficiency of new super computers, as well as challenging mathematicians and computer scientists to improve the technology and equations used for calculating π.