Interesting Calculations
π is very useful in circle geometry, but it also pops up in other areas of math, such as probability. It also makes an odd appearance while calculating the length of a meandering river. Here are some unexpected calculations involving π
Square-free Integers
π has a surprising circle free application to probability. The probability of randomly selecting a square-free integer out of the entire number line is 6/(π2).
An integer is square-free if it has only unique prime divisors, and therefore, isn't divisible by a perfect square. For example, 18 is not square free, because one of its factors is 9, and 9 is a perfect square. The prime factor 3 appears twice. On the other hand, 30=5*3*2 is square free, because all of its prime divisors are unique. It does not contain any perfect squares.
Relatively Prime Natural Numbers
The probability of two natural numbers (0,1,2,3,etc) being relatively prime is also 6/(π2). Two numbers are considered relatively prime if they have no factors in common greater than 1.
For example, 15 and 8 are relatively prime, because they have no common factors. 15 and 9 are not relatively prime, because they share the common factor of 3.
Meandering Rivers
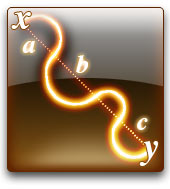
If you divide the length of a river by the direct distance between its source and where it reaches the ocean, then you will get a number that is quite close to π/2. This may seem surprising, but it makes sense when you consider the geometry involved.
The meanders and turns a river makes are roughly equal to semi-circles. The distance between the source and the end of the river (the doted line between x and y) is like adding up all the diameters of these semi-circles (a+b+c). Since the circumference of a circle divided by its diameter is π, the circumference of a semi-circle divided by its diameter is π/2. The glowing line represents the length of the river, and you can see that it is the sum of the circumferences of the semi-circles. When we divide this by the sum of the diameters of the circles (the distance between the source and the outlet of the river) we get π/2.