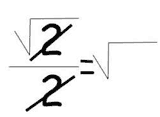Is there a mathematical theory of everything?

What makes a good theory?

In Gottfried W. Leibniz's philosophical essay Discours de métaphysique (Discourse on Metaphysics), he says that a theory has to be simpler than the data that it explains, otherwise it does not explain anything at all. A theory as long as the data is pointless. Given any random set of data we always have the ability to come up with a law for it, but this law is going to be just as complex as the data itself. Thus, the law is essentially useless.

Information Theory

This is one of the big principles behind information theory. Information theory deals with a quantity called the "algorithmic information content" of some data. This quantity is based simply on the size of the program (the law) we need to recreate a set of data. The longer the program needed, the more algorithmic information content the data has.

Here is where we extend Leibniz's ideas; given two programs to recreate the data, the simpler program with the least amount of algorithmic information is preferred (Occam’s razor). Also, the simpler the program, or theory, the better you understand the data. Comprehension is compression.

Examples

Consider the infinite series 1, 2, 3, 4, 5, etc. The program needed to recreate it would be very simple. Output the number 1, and add 1 to the previously outputted number to get the next number. The series does not have very much algorithmic information.

If instead you have an infinite and random series, there is no governing principle or law to recreate it. The program would have to be essentially as long as the number, because it has to specify exactly which digit comes next. Therefore, this number is irreducible, in other words, algorithmically random.

A Mathematical Theory of Everything is Impossible

Chaitin’s constant is one of these irreducible numbers. From this, we can conclude that a theory of everything for math cannot exist. This claim seems a bit shocking, but there is an surprisingly simple explanation. Consider the infinite bits of omega. Since omega is a mathematically defined and determined constant, whether each of these bits are a 0 or a 1 is essentially an infinite set of mathematical facts.

We know that these bits of mathematical fact cannot be derived from any principles simpler than the string of bits itself, so we have to conclude that math has infinite complexity. Therefore, we will never have a theory that will capture the entire world of mathematical truth.

Here in lies the philosophical implication: there are certain mathematical facts that are simply true for no reason. This is a startling contradiction to the principle of sufficient reason, the idea that there is a reason behind everything that occurs or exists.