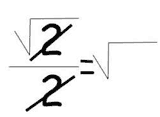A Divergence Proof

The following celebrated, yet quite simple, divergence proof of the harmonic series was originally done by Nicole d'Oresme in the 1300s. It relys on providing a lower bound on H_n (which is just a function that is always below H_n) and showing that this lower bound goes to infinity.

The Set Up

The proof begins by simply grouping the terms together in such a way that the last term in each grouping has a denominator with some power of 2, like so:

H_∞= 1 +1/2+ (1/3 +1/4) + (1/5+…+1/8) + (1/9+…+1/16) + ……

The Inequality

We know that this sum must be greater than:

1 +1/2+ (1/4 +1/4) + (1/8+…+1/8) + (1/16+…+1/16) + ……

because the bigger the denominator, the smaller the number.

Simplification

This new sum can be reduced to:

1+ 1/2 + 2/4 + 4/8 + 8/16 +….

or simply:

1+ 1/2 + 1/2 + 1/2 + 1/2 +….

Which we can easily see runs off to infinity.

The Comparison

Since H_∞ is always greater than this new sum we created, H_∞ must go to infinity also.