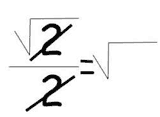An Irrational Proof

The proof that √2 is irrational is fairly simple, but has big implications for how we think about numbers. Hippasus may have been killed for his geometric proof, so here we’ll stick to an algebraic one.

The Proof

Assume that √2 is rational.

This means it can be expressed as m/n, where m and n are integers. Let m/n be in reduced form. This means that m and n have no common factors.

√2=m/n

√2n=m

2n²=m²

Since 2 times an integer equals m², m² must be even. (If 2 times an integer equals m², then one of m²'s factors must be 2, making it even.)

Since m² is even, m must be even. (If m ws odd then m² would be odd, since multiplying two odd numbers together alwys makes another odd number.)

This means we can express m as 2k (where k is any integer).

We plug 2k into the equation:

2n²=(2k)²

2n²=4k²

n²=2k²

This means n² is even, so n is even.

So we can express n as 2j (where j is any integer).

√2=m/n

√2=2k/2j

HEY! THAT"S NOT REDUCED!

At the start of the proof we said that m/n expressed √2 in reduced form. If m/n=2k/2j then m and n have the common factor 2, so clearly the fraction isn't reduced.

Our assumption led to a contradiction, so it must be wrong.

√2 cannot be rational.

√2 is irrational.